How to Snail Sort (the Right Way)

TL;DR: Snails are really Rubik’s Cubes in disguise

I’m not the type of person who loves algorithmic coding “challenges” for their own sake. Some of them can be fun (shoutout to Advent of Code), but nine times out of ten, I’d rather work on actual projects. That said, I do think such challenges are an excellent way to learn the ins and outs of a new programming language.

Recently, I’ve been exploring functional programming languages as a way to expand the way I think about problem solving, and to force myself out of my comfort zone. In particular, I’ve gravitated toward Elixir, which has proven particularly suited to some coding challenges and rather tricky for others.

Having to think in terms of recursion, pipelines and reducers for every problem certainly causes friction when you’re used to imperative programming, but sometimes this friction leads to discovering a much more elegant solution. A perfect example of this is the fun (but probably useless) sorting algorithm problem: the Snail Sort.

What is “Snail Sort” anyway? #

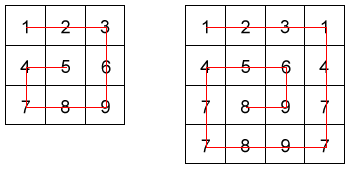
The Snail Sort is a sorting algorithm challenge found on sites such as Codewars. The idea is to come up with an algorithm that takes a 2D array and returns a flattened array, sorted in a clockwise spiral order, reminiscent of the spiral on a snail’s shell.

So, as can be seen from the image above, if given the following 2D array…

[[1, 2, 3],
 [4, 5, 6],
 [7, 8, 9]]

…your algorithm should return an single, flat array in this order:

[1, 2, 3, 6, 9, 8, 7, 4, 5]

The Naïve Approach #

In an imperative language, most people (myself included) would jump at the naïve procedural approach and call it a day:

1. Take the top row (first inner array).
2. For the length of the outer array, take the last element each inner array.
3. Take the last inner array, reversed.
4. Traversing backward over the outer array, take the first element of each inner array
5. Repeat until empty.

And while there is nothing wrong with this approach, I do think it is telling that this article is the top Google result for “Snail Sort” – this is simply the way that most of us are used to thinking.

Attempting the procedural method in Elixir #

In my initial attempt at solving this problem with Elixir, I’ll be the first to admit I immediately tried to apply the five steps listed above. However, attempting to translate procedural solutions to a functional programming language can be tricky — even uncomfortable! — and feels much like fitting a square peg into a round hole.

For starters, you don’t have traditional loops, so you need to make the decision early on how you’re going to “loop” through the arrays. Recursion? Reduce? Comprehension? Then, to make things even more complicated, all lists in Elixir are implemented as linked lists, so accessing elements in a list occurs in linear time. Want to get the last element in the list? Cool, that’ll be O(n).

With this in mind, I decided to use a combination of recursion and Enum.reduce/3 in my first solution. Below is a high-level summary of my process:

• Write a recursive function for a single rotation of the “spiral”.
• Break each step of the spiral into its own function that reduces the matrix (if needed).
• Each function accepts and returns a tuple containing a) the remaining matrix, and b) the new, sorted list.
  • This makes the functions easily pipeable and allows for easy pattern matching to determine if the matrix is empty at any step and exit the recursive loop (because Elixir doesn’t have return or break keywords).

defmodule Snail do
  def snail(matrix) do
    sort(matrix, [])
  end

  defp sort([], sorted), do: List.flatten(sorted)
  defp sort([head | tail], sorted) do
    sorted = sorted ++ head
    matrix = tail

    {matrix, sorted} =
      add_last_nums({matrix, sorted})
      |> add_bottom_row
      |> add_first_nums

    sort(matrix, sorted)
  end

  defp add_last_nums({[], _} = done), do: done
  defp add_last_nums({matrix, sorted}) do
    matrix
    |> Enum.reduce({[], sorted}, fn l, {m, s} ->
      {i, l} = l |> List.pop_at(-1)
      {[l | m], s ++ [i]}
    end)
  end

  defp add_bottom_row({[], _} = done), do: done
  defp add_bottom_row({[head | tail], sorted}) do
    {tail, sorted ++ Enum.reverse(head)}
  end

  defp add_first_nums({[], _} = done), do: done
  defp add_first_nums({matrix, sorted}) do
    matrix
    |> Enum.reduce({[], sorted}, fn l, {m, s} ->
      [i | l] = l
      {[l | m], s ++ [i]}
    end)
  end
end

Ultimately, I’m not upset with this solution. It works, and it’s fairly easy to see when each step occurs and what happens in each step. That said, while writing it I couldn’t shake the feeling that there had to be a better way. It wasn’t until about halfway through that I figured out the approach I should have taken from the start.

A More Elegant Solution #

So far in my journey to learning Elixir, I’ve discovered a trend that shows up whenever I try to solve a problem the same way I would in an imperative language. First, I get extremely frustrated because the tools I’m looking for are either not a part of the language or, if they are, they feel awkward to use.

Next, I try to bend the language to my will, only to find myself unsatisfied with the result. Oddly enough, the syntax and implementation of Elixir feel like they want to guide the programmer to solve some problems in a very specific (and often more efficient) way.

Ultimately, I end up taking a step back and looking at the problem from a different perspective. For me, this mindset shift often ends in an “aha!” moment and it certainly did in this case.

Snails are Rubik’s Cubes #

If you take a closer look at the snail sort diagram above, you might notice that the matrix we’re tasked with traversing looks suspiciously like one face of a Rubik’s Cube.

With this in mind, it becomes abundantly clear that all you need to do is take the first row, rotate the cube 90 degrees to the left and repeat (!!!) until there is nothing left to remove.

That’s it! No popping the last element of the lists, no traversing backwards – just “twist, remove, twist, remove” until it’s empty.

And the best part? It’s not even difficult to implement. Take a look at the following code (adapted from @simonvpe’s Codewars solution), which shows just how easily and elegantly this can be accomplished in Elixir:

defmodule Matrix do
  def horizontal_reflect(m), do: m |> Enum.reverse
  def transpose(m), do: m |> List.zip |> Enum.map(&Tuple.to_list(&1))
  def rotate_left(m), do: m |> transpose |> horizontal_reflect
end

defmodule Snail do
  def snail([]), do: []
  def snail([h | t]), do: h ++ (t |> Matrix.rotate_left |> snail)
end

# original matrix:
[[1, 2, 3],
 [4, 5, 6],
 [7, 8, 9]]

# after the matrix has been transposed (columns into rows):
[[1, 4, 7],
 [2, 5, 8],
 [3, 6, 9]]

# after the transposed matrix has been flipped over the x-axis:
[[3, 6, 9],
 [2, 5, 8],
 [1, 4, 7]]

# original matrix:
[[1, 2, 3],
 [4, 5, 6],
 [7, 8, 9]]

result = []

# step 1
[[4, 5, 6],
 [7, 8, 9]]

result = [1, 2, 3]

# after rotation 1:
[[6, 9],
 [5, 8],
 [4, 7]]

result = [1, 2, 3]

# step 2
[[5, 8],
 [4, 7]]

result = [1, 2, 3, 6, 9]

# after rotation 2:
[[8, 7],
 [5, 4]]

result = [1, 2, 3, 6, 9]

# step 3
[[5, 4]]

result = [1, 2, 3, 6, 9, 8, 7]

# after rotation 3
[[4],
 [5]]

result = [1, 2, 3, 6, 9, 8, 7]

# step 4
[[5]]

result = [1, 2, 3, 6, 9, 8, 7, 4]

# afer rotation 4
[[5]]

result = [1, 2, 3, 6, 9, 8, 7, 4]

# step 5
[]

result = [1, 2, 3, 6, 9, 8, 7, 4, 5]

Conclusion #

I don’t really have any closing remarks, other than hoping this change of perspective is as game-changing for someone else as it was for me. I’m in the business of sharing knowledge, and this felt a little too good not to share.

I don’t expect to become a functional programming expert overnight, and I recognize that this paradigm might not be the best for every problem. But, if I were to verbalize my goal for the near-future, it would probably look something like this:

Be the one who spins the cube, not the one who walks all the way around it.

🐌